April 24th, 2023
Something that we obviously needed to do, was to look at the behavior of real-world objects and how it can be modelled by physics equations. While the equations we looked at in-class do reflect how actual objects move, they do not capture enough of the complexity involved in real-life. For instance, while we talked about concepts like angular velocity, we never really took a look at how the application of force on a specific point would cause the object to rotate like how a box leaning too far off the edge of a table would rotate and fall off. For that, we took a look at the articles from Chris Hecker for the modeling of rigid body dynamics.
He starts off by covering the basic concepts, like the relationship between displacement, velocity, and acceleration as derivatives and integrations of each other in respect to time. He then goes and defines momentum as the summation of mass times velocity at every point, as well as centre of mass as the weighted average of the points of the object in respect to mass. There is also something called the centre of gravity, although it is commonly used interchangeably with centre of mass when the acceleration from gravity is uniform, as it is the weighted average of the forces instead of the mass. What he then derives, can be simplified as the fact that uniform acceleration acting on a body can be broken down to the application of force on a single point being its centre of mass, which is how we have been treating forces thus far in physics. One other property of the centre of mass, is that by dividing the object along that point, a uniform acceleration can be achieved by applying the same total force to both sides. The formulas he uses here are used in his next article which focuses on the rotational physics involved.
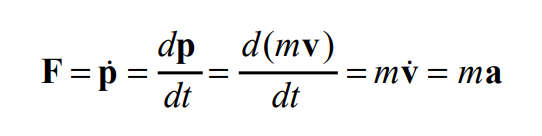
Force is the change in linear momentum, which is (mass * acceleration).
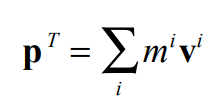
The sum of all momentum (mass * velocity) gives you the total momentum.
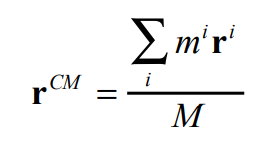
Centre of mass acts as a weighted average of the points as each point is a percentage (point mass / total mass) of the object.
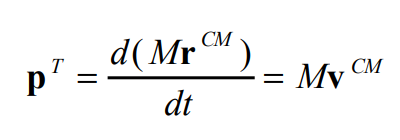
Relation between momentum and centre of mass.
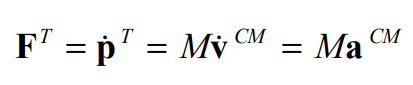
Derivation of the relation between centre of mass and force at point.